工程能力：Cp/Cpk No.1 | 工程能力評価 Cp/Cpk

生産設備の能力

生産設備の能力を示す数値は２つあります。

生産能力＝生産数量
工程能力＝品質
- 良品を生み出す能力を定量化したもの

工程能力指標がなぜ必要か

不良率「ゼロ」は目標とされますが、下記のような理由で現実に不良率ゼロを達成するのは困難です。

技術的限界
コスト

そこで、経済的、技術的に合理性の高い不良率を予測、制御するための数値的判断材料として工程能力指標が使われます。

工程能力：Cp、Cpkについて

Cp/Cpkとはそもそも何の指標でしょうか。

Cp:	工程のバラつきを表す(予測する)統計指標
Cpk:	工程のバラつきと偏りをを表す(予測する)統計指標

統計を根拠として工程能力を定量化した指標がCp/Cpkです。
主にロット生産がメインで数千個、数万個といった単位で生産される量産部品工程で広く使用されているいます。
基本的な計算方法は決まっていますが、実戦での運用には工夫が必要です。

ヒストグラム

ヒストグラムは工程能力を視覚的、感覚的に理解する重要なツールです。
ヒストグラムの味方が分かると、工程能力指数の数字を見るより直観的にデータに対して多くの事を読み取れるようになります。

ヒストグラムを理解するため下記に50個のサンプルデータを用意します。
※実際は数千、数万個の抜取データとなる。
　例：100個１ロットで各ロット5個ずつの抜取、等。

1	100.03	11	99.975	21	99.991	31	99.99	41	99.995
2	100.028	12	99.968	22	100.038	32	100.002	42	99.986
3	99.999	13	99.979	23	100.001	33	99.972	43	100.014
4	99.957	14	99.984	24	100.03	34	100	44	100.016
5	99.988	15	100.021	25	100.05	35	99.973	45	99.968
6	99.995	16	100	26	100.014	36	99.974	46	99.97
7	99.996	17	100.001	27	100.005	37	99.978	47	99.988
8	100.027	18	99.982	28	100.002	38	100.041	48	100.005
9	99.992	19	100.005	29	100.015	39	100.005	49	99.959
10	99.97	20	100.005	30	100.035	40	100.046	50	100.021

クラス

ヒストグラムを描画するためには、最初にデータをクラス(階級)に分ける
- EXCEL等で描く場合は通常、意識することなく、自動でクラス分けされる。
- クラス分けの計算方法は複数あるが、EXCELやPythonはスコットの正規化基準ルール (Scott’s normal reference rule)を採用しているようです。
- 各クラスは等間隔に区切られており、それぞれのクラスに該当する数値が何個発生しているかを数えます。

階級	クラス1	クラス2	クラス3	クラス4	クラス5	クラス6
発生数	2	11	11	15	6	5
範囲	99.948~ 99.965	99.965~ 99.982	99.982~ 99.999	99.999~ 100.016	100.016~ 100.033	100.033~ 100.050

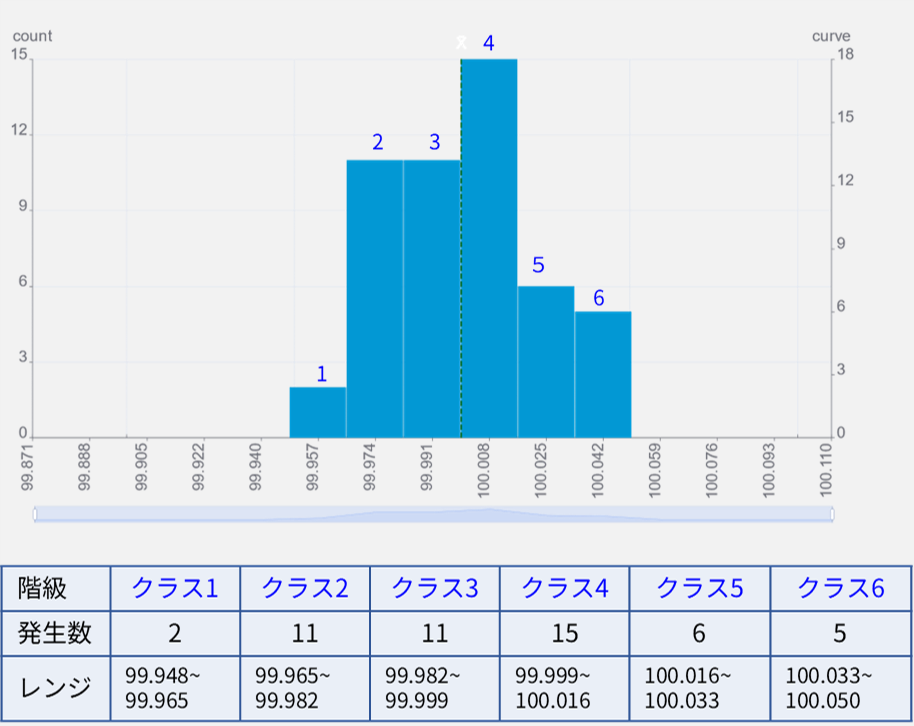
ヒストグラムの書き方

1クラスのデータを1つの棒グラフで描画する
下図は6つの棒グラフ(クラス)に分かれている

※右図の例はスコットの正規化基準ルール (Scott’s normal reference rule)を採用して計算している
　がグラフを見易くするため数式に修正を加えており、EXCELとはクラス数が若干異なる。

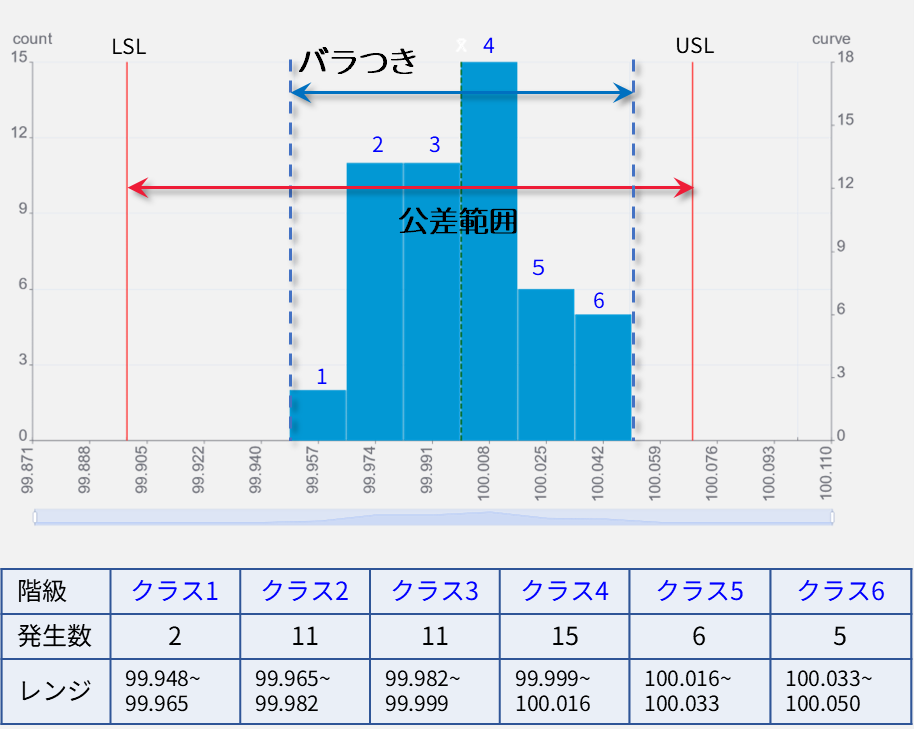
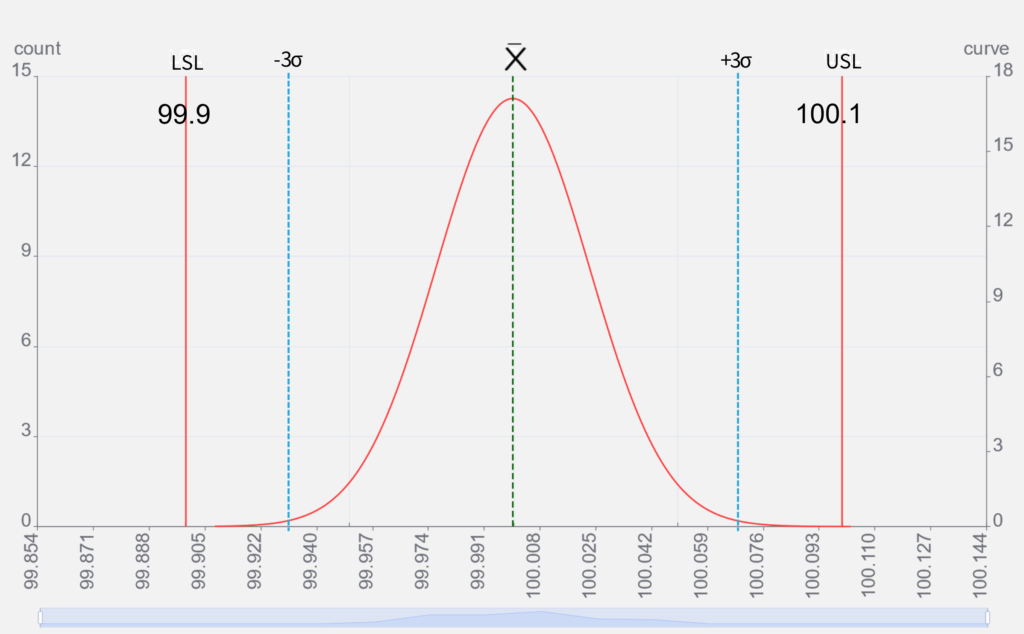
左のグラフは前出のグラフに

上方仕様限界 USL： Upper Specification Limit
下方仕様限界 LSL： Lower Specification Limit

の2つを加えたものです。

データのバラつきの幅と公差範囲を比較すると、50個のデータ全てが公差内にあり、良好そうに見えます。

「この状態で量産へ移行したら結果はどうなるか？」

というのを予測するのが工程能力Cp/Cpkで、量産を開始するか否かを判断する基準になります。

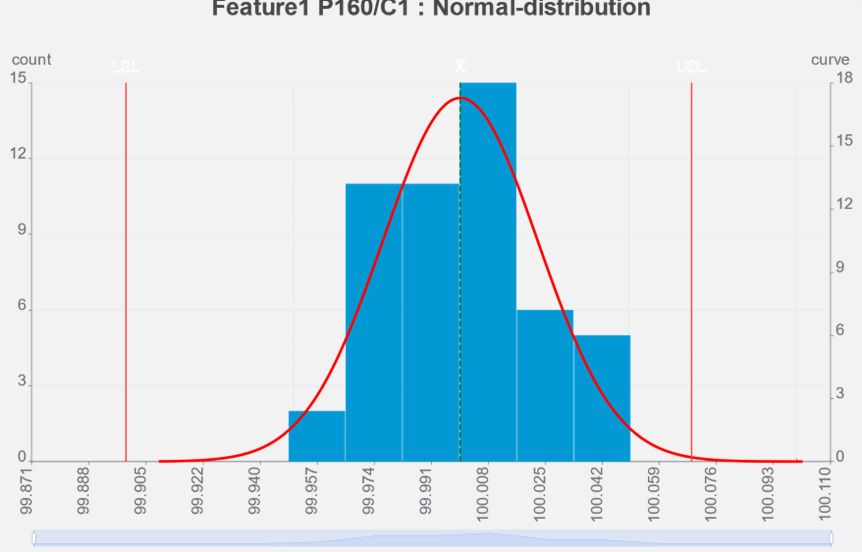
分布曲線

左のグラフは前出のグラフに

分布曲線

のを加えたものです。

この分布曲線は正規分布曲線（ガウス曲線、ガウシアンカーブ等呼び名複数あり）と呼ばれ、EXCELなどの表計算ソフトでも描画できます。

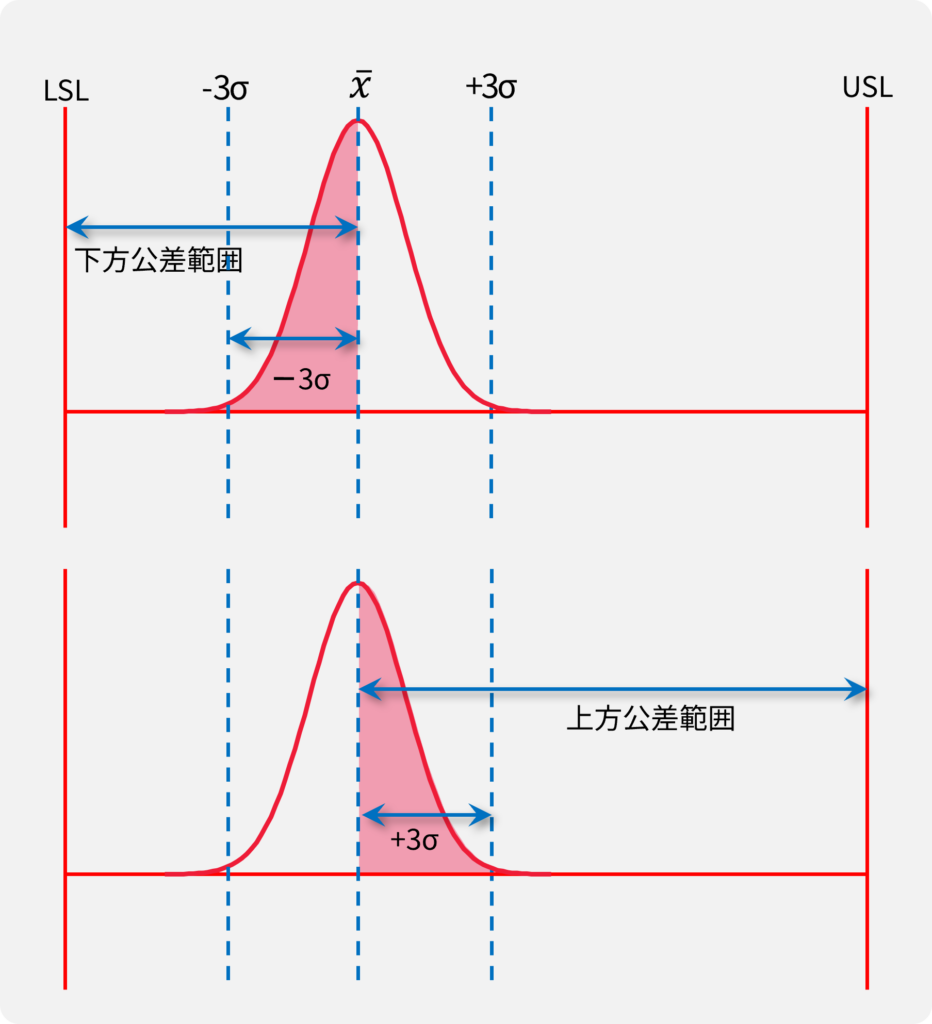
正規分布の性質

一般的にデータのバラつきは正規分布曲線に沿うと言われていますので、この棒グラフは分布曲線の形に沿うように増加すると予測できます。

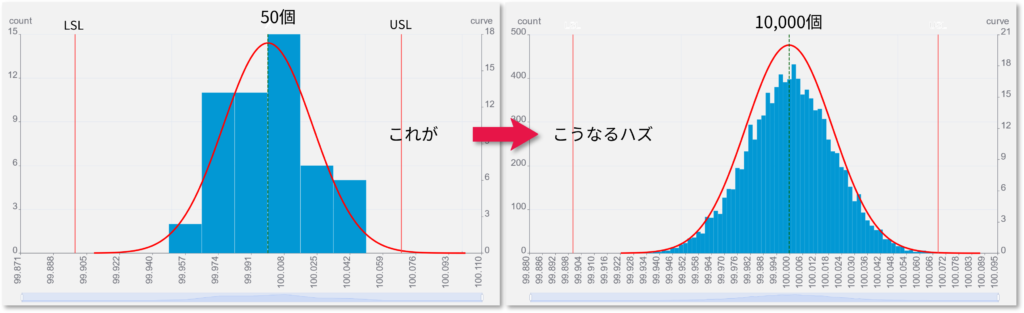
σの意味

グラフがこの分布曲線に沿うのであれば、この分布曲線の幅と公差範囲を比較すれば、どの程度公差外が発生するか予測できます。

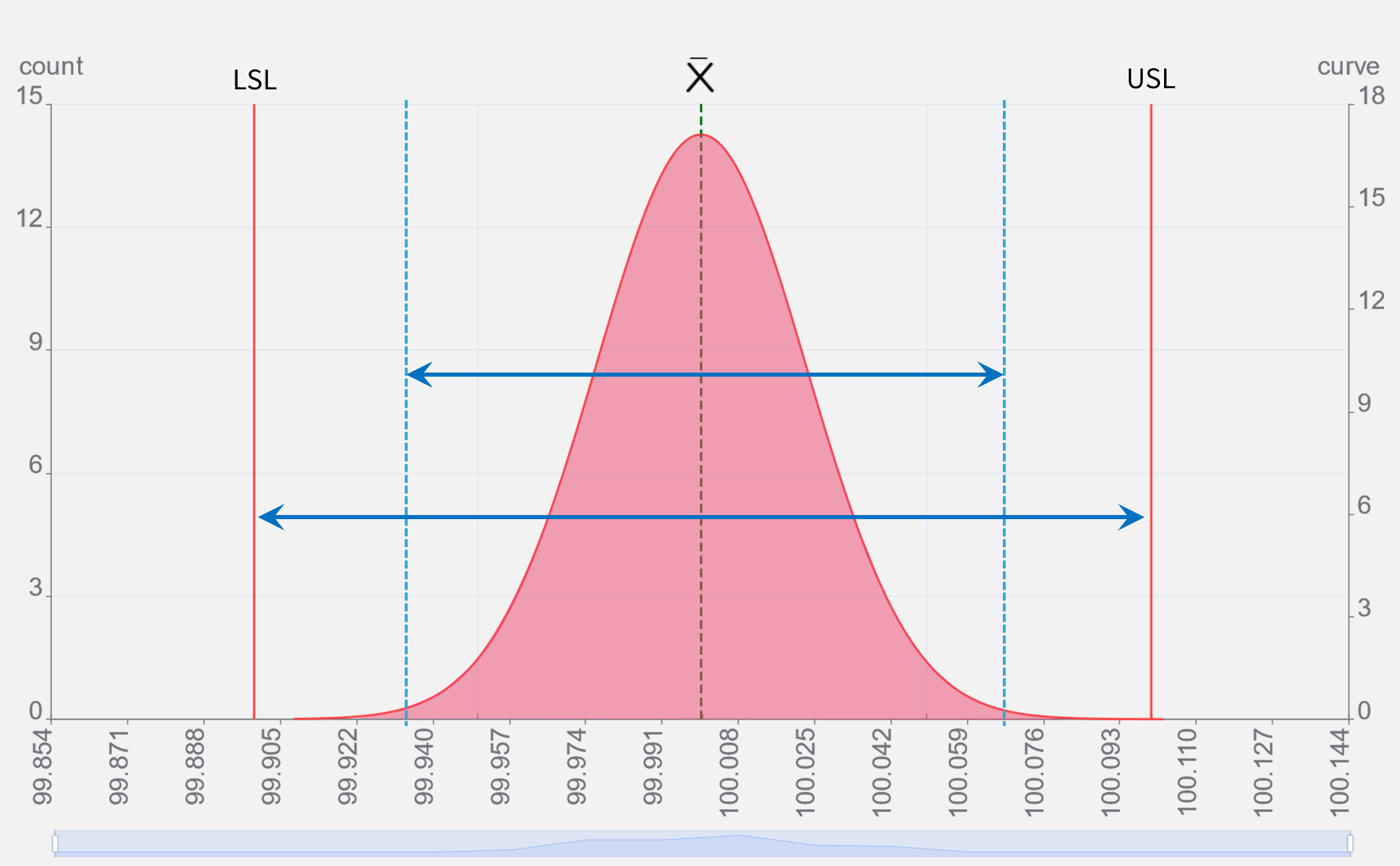
σの算出

正規分布曲線からは標準偏差σが計算できます。

±1σ(σ2つ分)は曲線内面積の68.27%をカバーする事が分かっています。

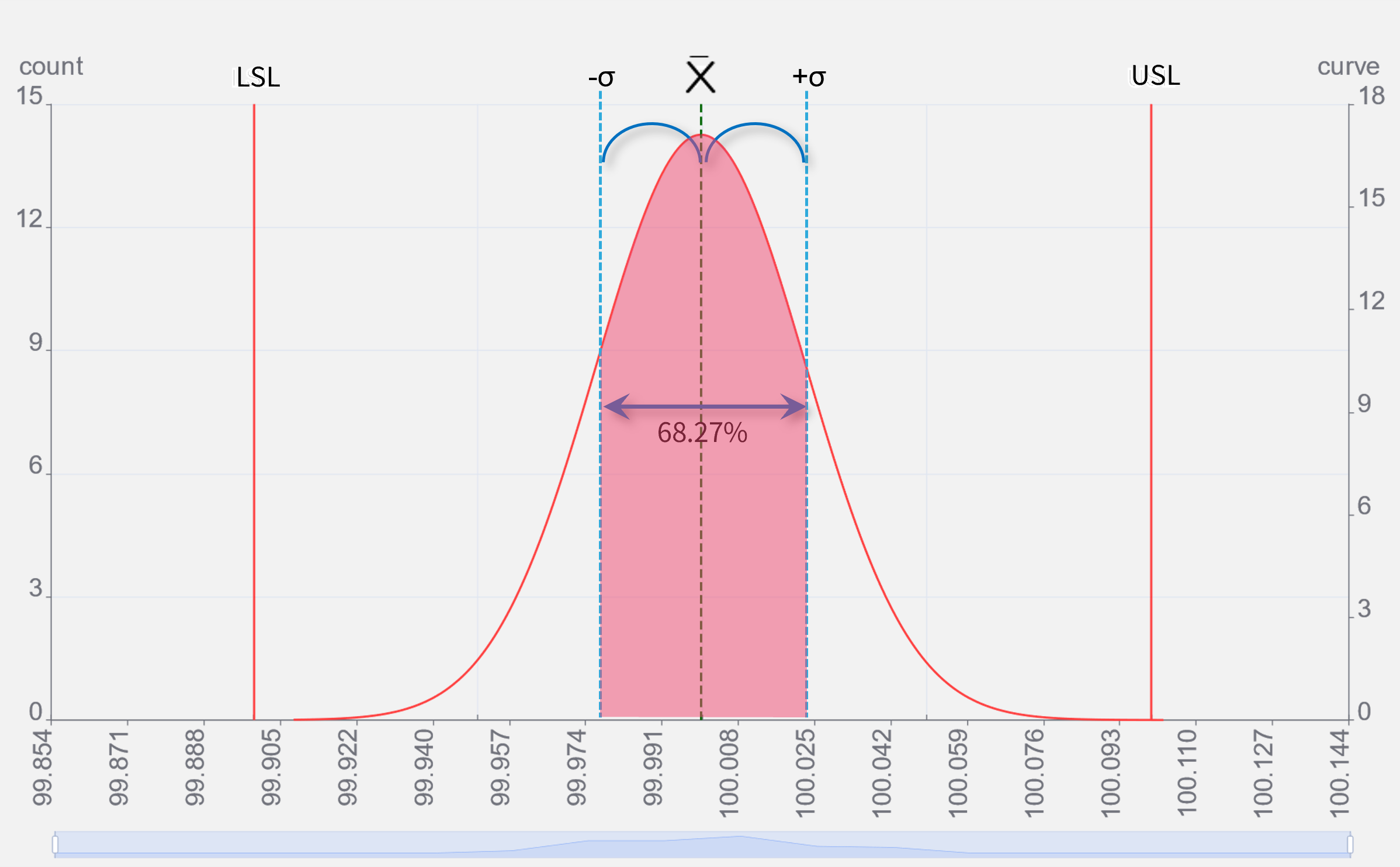
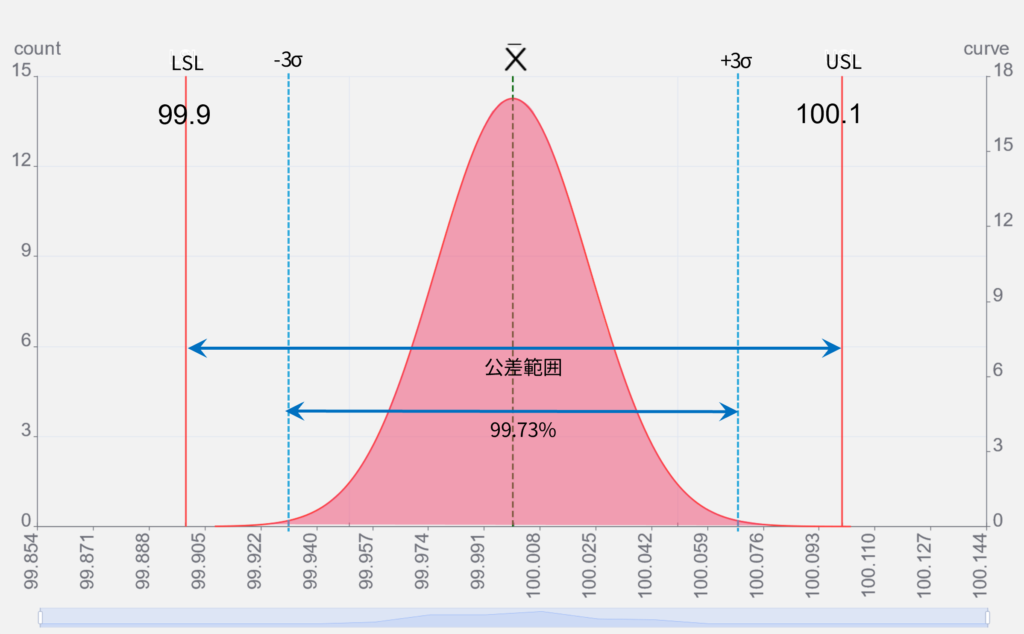
±3σの意味

σは6倍するだけで、分布曲線のほぼ全て(99.73%)の範囲を簡単に算出する事ができるので、公差との比較対象として都合がよい指標です。

なぜ100%の範囲を使わないのか？
実際のデータには必ず外れ値が存在します。全データの最大、最小範囲をもって公差との比較対象としてしまうと、入力ミスや検査装置、測定機器の異常で発生した外れ値も範囲に含まれてしまうため、それらを除外したデータを対象とします。

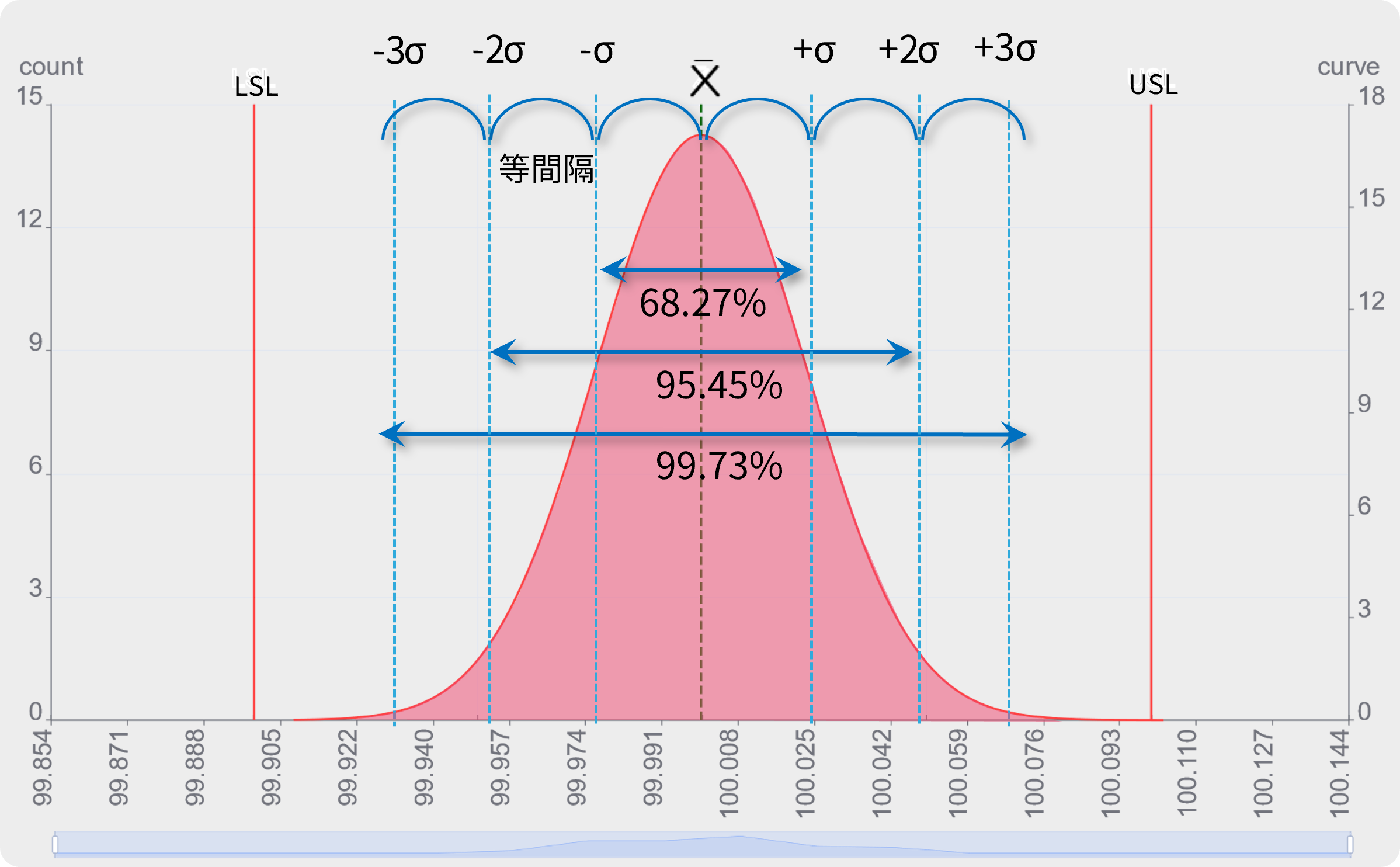
±3σの範囲 VS 公差範囲

本ケースでは、データを取り続けると99.930～100.068の間にほぼ全ての値が入るという予測されます。
1000個データを記録した時、±3σ外側にデータが発生する確率上1000個中2.7個、つまり3個以下です。

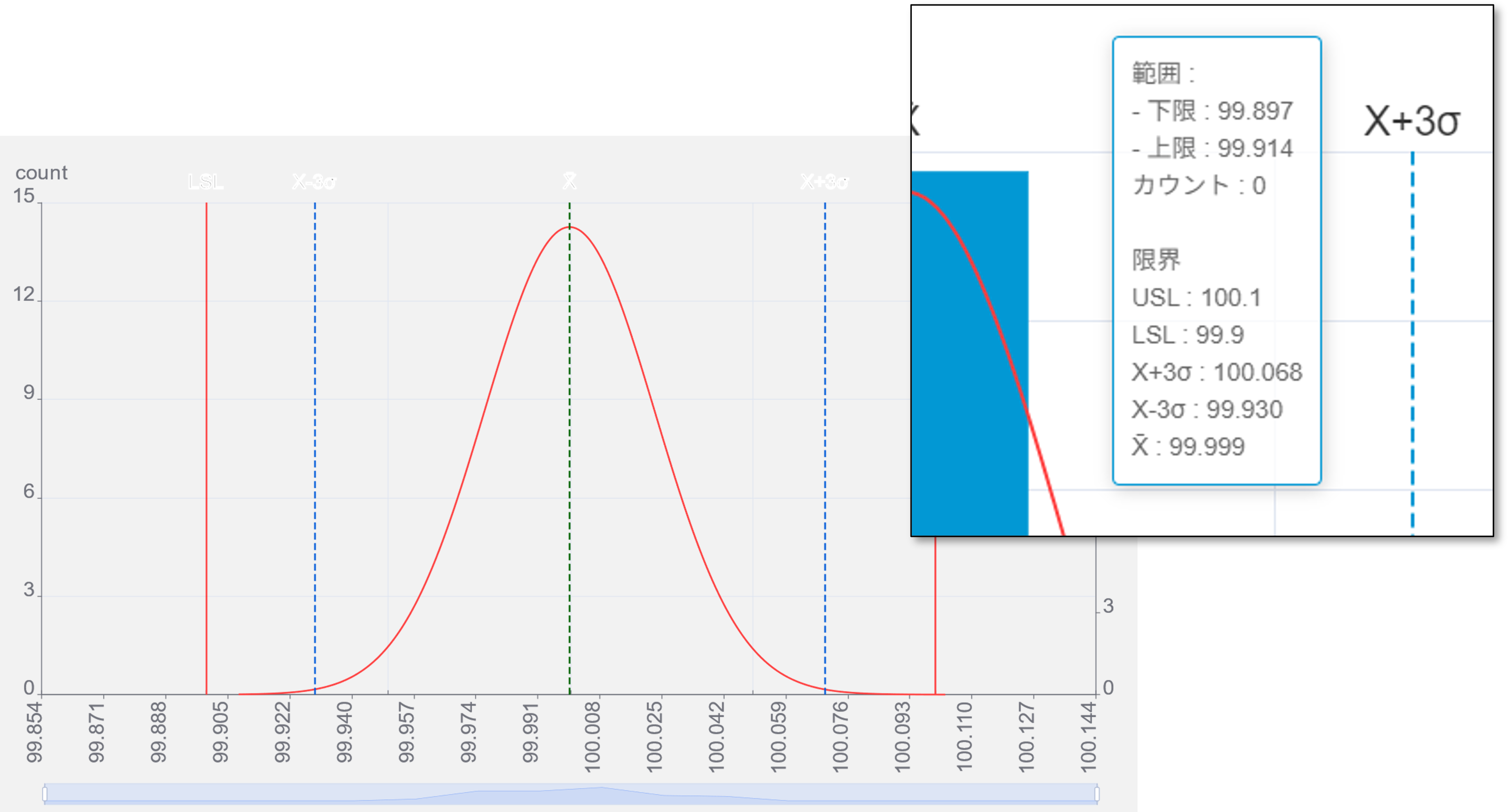
予測と結果

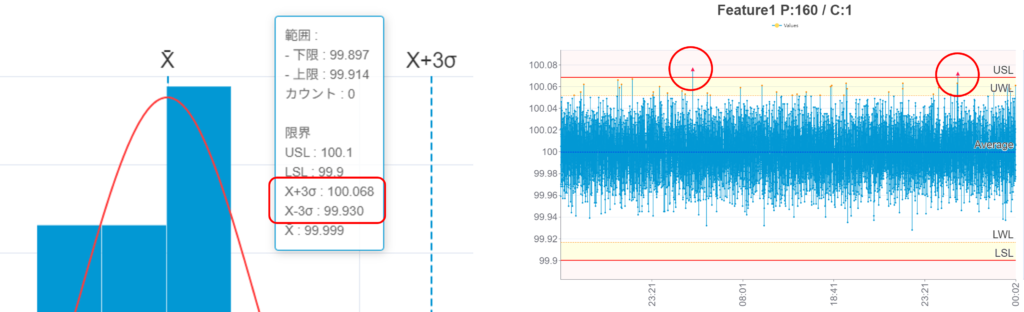
データ50個の段階で予測したデータのバラつき範囲は99.930～100.068でした(左図)。1000個までデータを観測した結果(右図)で、±3σの範囲外に出たのは2個となったので、このケースでは概ね予測通りの結果となりました。

CP

Cpの計算

3σの幅と、公差(USL-LSL)の幅の比較してきましたが、この比較を数値として表すのがCp/Cpkです。

計算方法

標本標準偏差を計算する
Cpを計算する

Cpの意味

Cp=1.429は、

「バラつき範囲が公差範囲に約1.4個入る」
「公差範囲はバラつき範囲より約1.4倍大きい」

のように認識すると感覚的に覚えやすい。
一般的に良好とされるのは1.33以上です。より厳しい基準では1.67、2.0などの合格ラインを設ける場合もあります。

Cpのまとめ

■

Cpは公差範囲との相対評価

■

Cpが小さい＝(公差に対して)バラつきが大きい

■

Cpが大きい＝(公差に対して)バラつきが小さい

Cpの性質

■

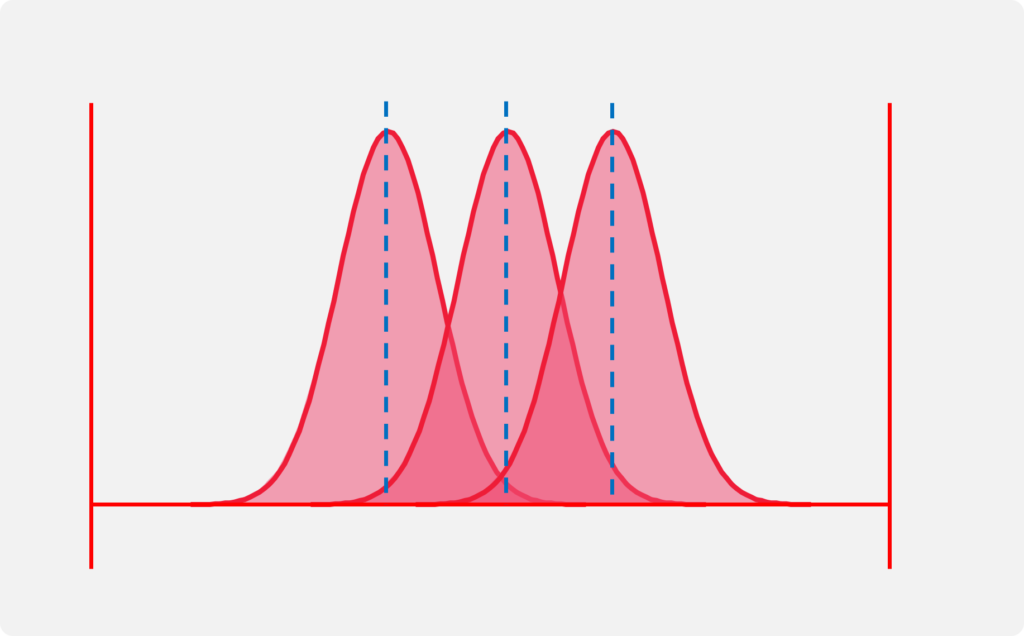
Cpは分布の位置を問題にしない

●

下図の3つのヒストグラムのCp値は全て同じ

■

Cpkは分布の位置によって値が変動する

Cpk

■

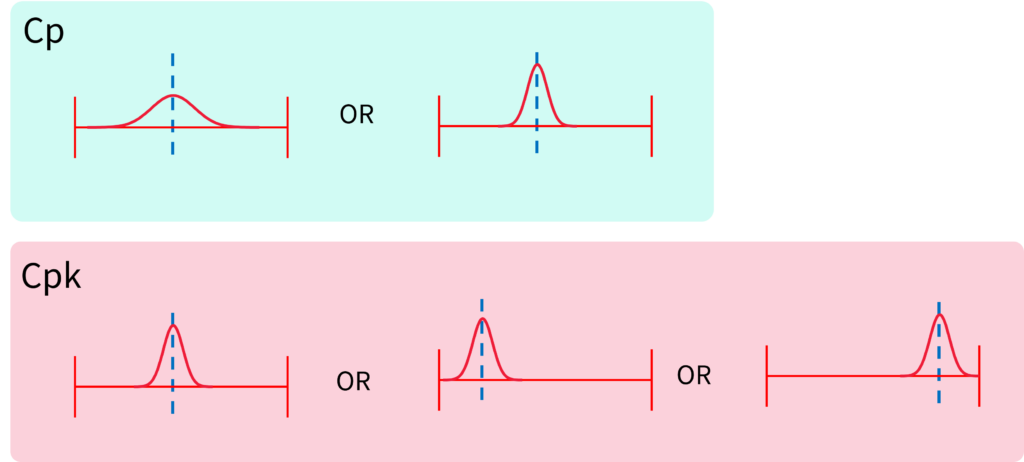
Cpは分布の幅(バラつき)を評価

■

Cpkは分布の幅と「位置」も評価

Cpkの計算

Cpkは分布を平均から上と、平均から下の2つに分けて評価します。
Cpl¹(下方)、Cpku²(情報)をそれぞれ計算し、小さい方の値をCpkとして採用します。

実際に計算してみます。

Cpの計算で、標準偏差は0.02332と計算出来ています。平均は99.9とします。

PPMとの関係
CpkからPPM（パーツパーミリオン）の不良率を計算する事も出来ます。

Cpkの性質

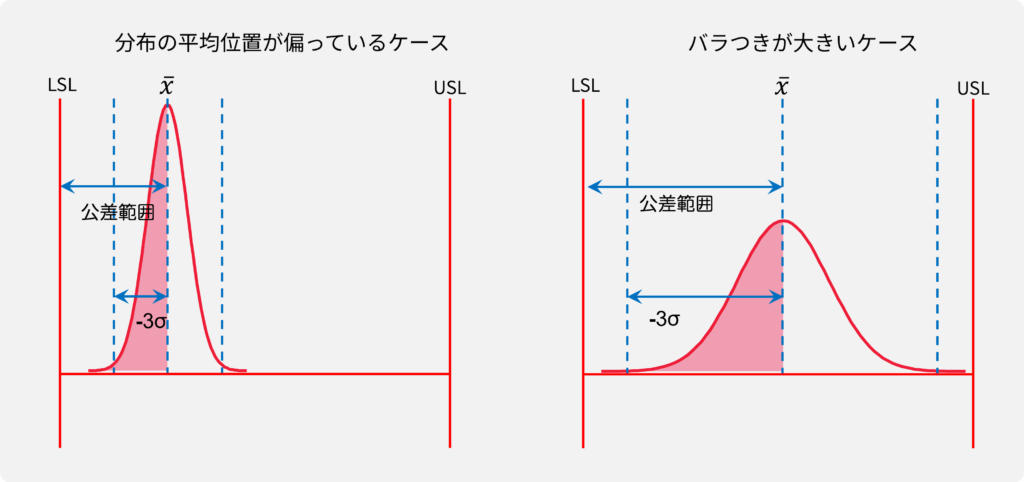
Cpkが小さくなる(悪化する)原因は2つあります。

■

バラつきが大きい

■

分布の平均位置が偏っている

この２つの場合(または2つの複合)はいずれもxbar-LSL/3σ(分子/分母)の差が小さくなるため、Cpkが小さくなります。

Cpkのまとめ

■

Cp/Cpkは公差範囲との相対評価

■

Cpk小＝バラつきが大きい、分布の中心位置が規格値から±どちらかに偏っている、又はその両方。

■

Cpk大＝バラつきが小さく、かつ分布の中心位置が大きく偏っていない。

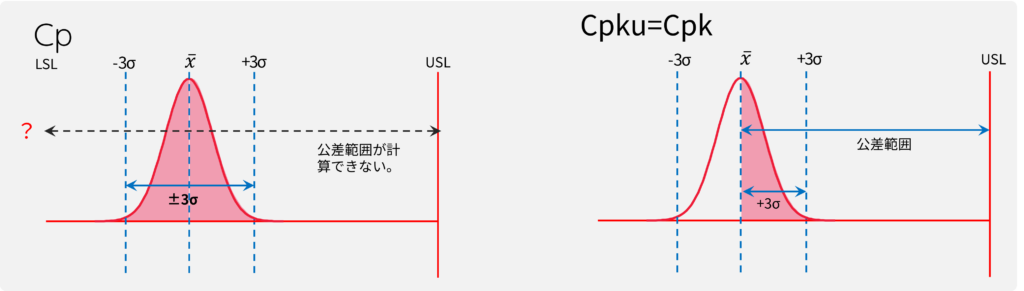
Cpで評価できないケース１:片側規格

片側規格の場合、LSLまたはUSLのどちらかが存在しない為、Cpが計算できません。
従って、Cpk³のみを算出します。

■

片側規格の場合、Cpkだけで評価する

Cpで評価できないケース１:片側公差(自然限界)

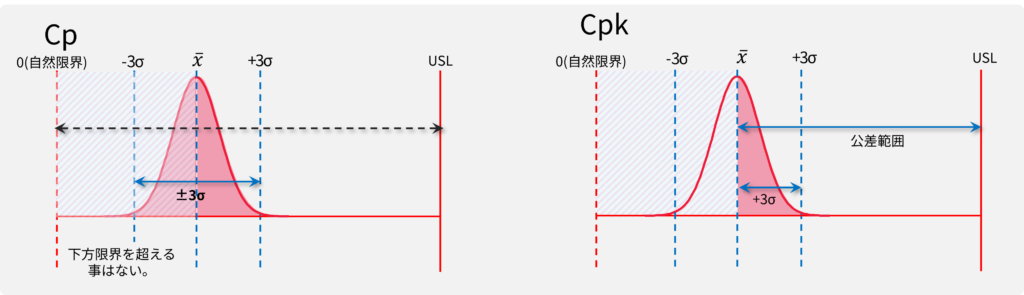
真円度、平面度、直角度などの幾何公差の場合、片側公差になり、LSLは0(ゼロ)になります。片側規格の場合、LSLもUSLも存在するので、Cpを計算する事は出来ますが、どれだけバラついても限界を超える事はあり得ません(データ入力ミスなどで超える事はあり得ますが。）このような限界値を自然限界と呼びます。一般的に下図のようなケースになりますが、自然限界の場合LSL=目標値になるので、LSL方向に近い値は何ら問題の無い値です。よってLSL方向へバラつく事は考慮する必要がありません。従って、Cpkのみ⁴を算出します。

■

自然限界の方向へのバラつきは限界値を超える事が無いので問題視しない。

■

Cpを計算しても意味がない。

■

自然限界ではない方の半分を計算し、Cpkとして採用する。

非正規分布

前項で真直度等の幾何公差はLSLが自然限界となる事を説明しました。このようなデータはプラス方向にのみバラつきます。
実はこのようなデータは分布の形が正規分布に沿いません。

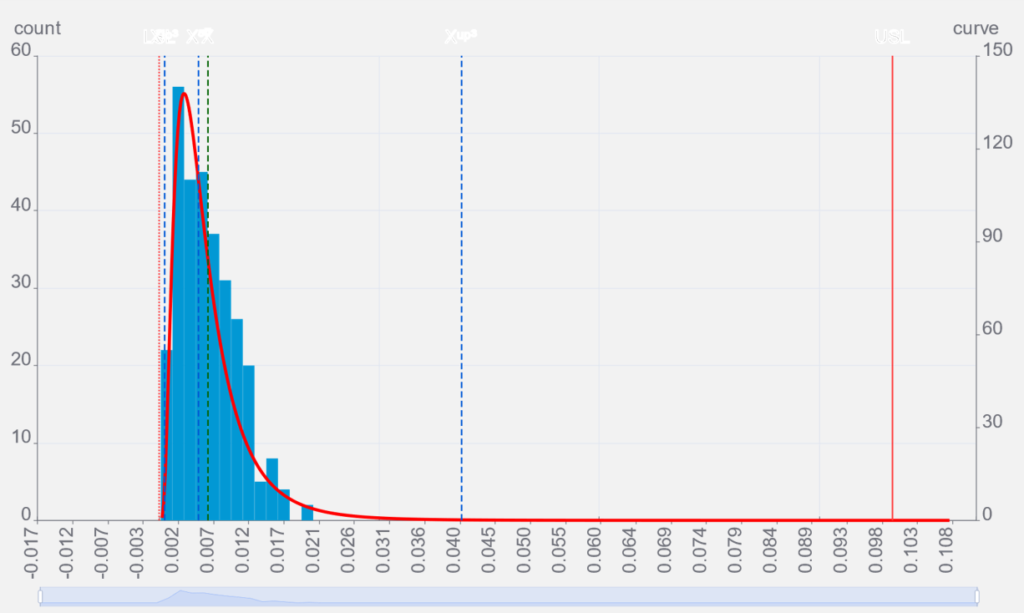
非正規分布の工程能力計算は正規分布のように標準偏差を使った計算ができません。非正規分布の計算については工程能力：Cp/Cpk No.2で解説しています。

以下脚注

uはUpper(上方)のu ↩︎
lはLower(下方)のl ↩︎
CpkもCpkl、Cpkuのどちらかが計算出来ない為、「Cpkが計算できないのでCpのみ計算する」とされている場合もありますが、いずれの場合もCpkl、Cpkuのどちらかだけを計算し、Cpk(Cp)とするという考え方で、結局のところ計算式は同じです。能力指標の呼称にとらわれず、何を評価しているか理解する事が大切です。片側規格の場合Cp=Cpkと考えて差し支えありません。 ↩︎
自然限界の場合Cpkl、Cpkuのどちらかを計算する意味がありません、「Cpkが計算できないのでCpのみ計算する」とされている場合もありますが、いずれの場合もCpkl、Cpkuのどちらかだけを計算し、Cpk(又はCp)とするという考え方で、計算式は同じです。 ↩︎